movimiento ondulatorio

MOVIMIENTO ONDULATORIO: 
Cuando golpeamos una campana ó encendemos una radio, el sonido se oye en
puntos distantes de la campana ó de la radio. El sonido se ha transmitido a través del
aire. Si estamos en la playa y un bote pasa velozmente a cierta distancia de la orilla
sentimos al cabo del tiempo la onda producida por su movimiento. Cuando se
enciende la lámpara del cuarto, éste se ilumina. Aunque el mecanismo físico puede
ser diferente para cada uno de los procesos mencionados todos ellos tienen una
característica en común, son perturbaciones físicas producidas en un punto del
espacio que se propagan a través del mismo y que se reciben en otro punto. Todos
estos procesos son ejemplos del movimiento ondulatorio cuya característica esencial
es que en él se transmite una propiedad de un lugar a otro a través de un medio, pero
el medio en sí mismo no se traslada, es decir no se traslada masa sino energía.

Descripción matemática del movimiento ondulatorio: 
 Pasemos a describir matemáticamente este fenómeno. Consideremos una
función x=f(x) representada gráficamente por la curva de la figura 2.1. Si
reemplazamos x por x-a, obtenemos la función x=f(x-a). Evidentemente la forma de la
curva no ha cambiado sino que se ha transladado sin deformación hacia la derecha, si
a es positiva, una cantidad a. Análogamente x=f(x+a) corresponde a un
desplazamiento hacia la izquierda. Si hacemos a=vt donde t es el tiempo, obtenemos
una curva viajera; esto es x=f(x-vt) representa una curva que se mueve hacia la
derecha con velocidad v, llamada velocidad de fase.

Podemos concluir entonces que la expresión matemática 

 x ( x,t) = f (x ± vt)

es adecuada para describir una situación física que se propaga sin deformación en el 

eje X; este es el llamado movimiento ondulatorio. La cantidad x=f(x,t) puede 

representar diversas cantidades físicas, tales como la deformación en un sólido, la 

presión de un gas, un campo eléctrico ó magnético, etc.

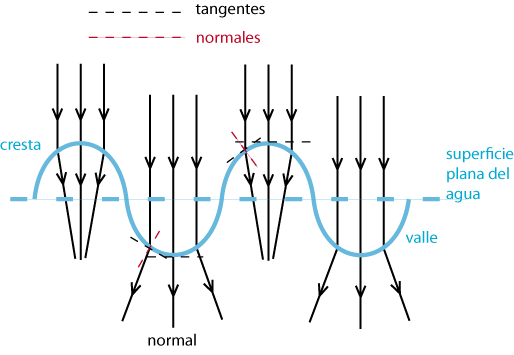
En una onda la perturbación puede ser perpendicular ó paralela a la dirección de propagación. Según esto distinguimos entre ondas transversales, donde la perturbación física es perpendicular a la dirección de propagación, caso del campo electromagnético, y ondas longitudinales con la perturbación paralela a la dirección de propagación, caso por ejemplo del sonido. Existen casos de movimientos ondulatorios combinación de transversales y longitudinales, como por ejemplo las ondas superficiales del agua tal y como se muestra en la figura 2.2. Podemos tambien tener una onda que ocupa todo el eje X, denominada onda continua, ó una onda que empieza y acaba en puntos determinados del espacio que se denomina tren de ondas ó pulso, esquematizadas ambas en la figura 2.3.

Ecuación diferencial del movimiento ondulatorio: 

 El proceso físico que gobierna el movimiento ondulatorio estará regido por 

leyes dinámicas, características de cada proceso, y que pueden expresarse en forma 

de ecuaciones diferenciales, tal y como ya vimos para el movimiento oscilatorio. Nos 

proponemos en este apartado encontrar una ecuación diferencial aplicable a todo tipo 

de movimiento ondulatorio de tal forma que cada vez que veamos que una magnitud física satisface tal ecuación podemos estar seguros que se 

propaga a través del espacio con velocidad definida y sin distorsión. 

 La ecuación diferencial que describe el movimiento ondulatorio que se propaga 

a una velocidad v y sin distorsión según las direcciones –X ó +X.

CLASIFICACIÓN DE LAS ONDAS:

- Atendiendo a su naturaleza:

Ondas mecánicas: requieren un medio material para propagarse, no se propagan en el vacío (son las que se propagan en una cuerda, en la superficie del agua, en el sonido, etc.)

Ondas electromagnéticas: no requieren un medio material para desplazarse. Se propagan en el vacío (RX, UV, IR, luz visible,...)

- Si asociamos una función de onda ð para describir formalmente una onda, según ðdependa de una, dos o tres coordenadas hablaremos de una, dos o tres dimensiones.

- Otra clasificación es atendiendo a su dependencia temporal. Destacan en este sentido las denominadas ondas armónicas, que son las que tienen una dependencia armónica o sinusoidal con el tiempo, y ondas con dependencia temporales de carácter más general.

- Otra subdivisión es la de ondas transversales y longitudinales según que la perturbación consista en una variación perpendicular o longitudinal a la dirección de propagación:

Ondas transversales: serían las electromagnéticas o las generadas en una cuerda.

Ondas longitudinales: serían el sonido y en general todas las que se propagan en medios fluidos.

- Teniendo en cuenta la dualidad onda-corpúsculo y el comportamiento simétrico de la naturaleza, puede pensarse que la materia exhiba esa dualidad

De Broglie estableció que las ondas asociadas a la materia debían estar gobernadas por las mismas ecuaciones que en el caso de la luz. V=E/h y ð=h/p (p= momento lineal; E= energía de la partícula). La longitud de onda de las ondas solo será relevante para valores de p, del orden de h.

AMPLITUD, LONGITUD DE ONDA, FRECUENCIA Y PERIODO DE UNA ONDA:

- Movimiento ondulatorio es la propagación de un movimiento vibratorio en un medio elástico.

- Amplitud es la máxima separación de la posición de equilibrio. A= elongación máxima.

- Longitud de onda, ð, es la distancia que separa dos puntos consecutivos que tienen igual fase. Dos puntos tienen igual fase si tienen el mismo estado de vibración y la misma separación relativa.

- Periodo, T, es el tiempo que tarda la vibración que se propaga en recorrer un espacio igual a la longitud de onda. Coincide con el tiempo que tarda el punto vibrante en realizar una oscilación completa.

- Frecuencia, ð, es el número de ondas que se propagan en un segundo. Este número coincide con el de vibraciones completas realizadas por segundo.

PRINCIPIO DE HUYGENS

El principio de Huygens proporciona un método geométrico para encontrar, partiendo de la forma conocida de un frente de onda en un cierto instante, la forma que tendría en otro instante posterior.

El principio establece que cada punto de un frente de ondas puede considerarse como manantial de pequeñas ondas secundarias, que se propagan en todas direcciones desde sus centros con la misma velocidad de propagación de la onda. El nuevo frente de onda se encuentra, entonces, construyendo una superficie tangente a las ondas secundarias; o sea, es la envolvente de estas ondas secundarias.

El frente de onda inicial es SS. Para encontrar la forma del frente de onda al cabo de cierto tiempo t, se constituye cierto número de circunferencias de radio r= vt, cuyo centro se encuentra sobre S-S'. La envolvente de estas ondas secundarias es la curva S' S', que es el nuevo frente de ondas.

La ausencia de una onda hacia atrás la explica Fresnel postulando el carácter inactivo de las mismas: las ondas secundarias solo son activas en los puntos de tangencia con las envolventes, debido a que en los otros puntos las interferencias entre ellas son totalmente destructivas.

La representación es válida para las ondas mecánicas, pero en cambio carece de significado físico para las ondas electromagnéticas, que se propagan en el vacío, donde no hay soporte material que permita la aplicación del principio de Huygens.

REFLEXIÓN Y REFRACCIÓN

Cuando una onda incide sobre una superficie que separa medios distintos, por lo que la velocidad de la onda es diferente en cada uno, se originan dos ondas: una que retrocede hacia el medio del cual procede (onda reflejada), y otra que se propaga en el segundo medio (onda refractada).

Se cumplen las siguientes leyes experimentales:

Los rayos incidente, reflejado y refractado están en un mismo plano, que es normal a la superficie de separación, y por lo tanto contiene a la normal V.

Los ángulos de incidencia y refracción son iguales. î=â'

3.Ley de Snell: el cociente entre los senos de los ángulos de incidencia y de refracción es constante. Sen î/Sen â=n21. La constante n21 se denomina índice de refracción del medio 2 con respecto al 1. Si para los medios 1 y 2 las velocidades de la onda son V1 y V2n21=n2/n1=V2/V1 entonces Sen î/Sen â=n21=n2/n1 que también se puede poner de la forma n1·Sen î =n2·Sen â. Si n2>n1 (n21>1) entoncesSen î>Sen â o lo que es los mismo î>â, por lo que el rayo refractado está angularmente más cerca de la normal que el rayo incidente. Por el contrario si n1>n2 el rayo refractado se aleja de la normal. Existe un ángulo crítico para la incidencia denominado ángulo límite, ð, tal que cuando î=ð entonces â=ð/2, lo que significa que el rayo refractado es paralelo a la superficie de separación. Para valores de ángulos de incidencia superiores a ð, se produce el fenómeno denominado reflexión total, no hay onda refractada, reflejándose íntegramente hacia el medio 1.

El movimiento ondulatorio: 

Todos tenemos una noción intuitiva sobre los movimientos ondulatorios. Estas 

palabras traen a nuestra mente la imagen de las vibraciones que se transmiten  por la cuerda de una guitarra o las olas marinas que van a morir a la playa. 

Hoy en día sabemos que fenómenos tan esenciales para nosotros como la luz 

y el sonido poseen una clara naturaleza ondulatoria.. 

Los fenómenos ondulatorios son un medio de transporte de energía  ampliamente usado por la Naturaleza, de forma que su estudio ocupa  necesariamente un lugar importante en la Física. 

Objetivos: 
Comprender la noción general de onda como transmisora de la energía  asociada a una vibración y algunas magnitudes comunes a todas las  ondas como longitud de onda, amplitud, frecuencia, periodo y  velocidad de propagación. · Clasificar las ondas adecuadamente por la relación entre la dirección de 
la vibración y la de propagación, así como por su propagación en una o 
más dimensiones. · Poder utilizar la ecuación de ondas para predecir el estado de vibración  de un punto alcanzado por las ondas. · Entender las leyes que gobiernan algunas propiedades de las ondas 
como reflexión, refracción, difracción, interferencia y polarización. · Entender la noción de intensidad y poderla aplicar al cálculo de 

intensidades a diversas distancias del foco y con diferentes grados de  absorción por el medio. · Entender el efecto que produce el movimiento relativo de foco y  observador sobre las ondas observadas.

Las dimensiones de las ondas: 
Las ondas que produce una piedra al caer  en un estanque se propagan en dos 
direcciones, a lo largo y ancho del 
estanque.  Las ondas luminosas de la 
bombilla de la derecha se propagan en las 
tres direcciones del espacio. 
Son ondas bidimensionales y 
tridimensionales respectivamente. 
Algunas propiedades de las ondas,, de validez muy general, se pueden 
estudiar a partir de ondas unidimensionales que se propagan en una sola 
dirección y son más fáciles de analizar.  Pulsemos el botón avanzar para 
estudiar este tipo de ondas.

Conclusiones sobre las propiedades de las ondas: 
Cuando las ondas encuentran un obstáculo a su propagación,  se produce la reflexión. 
La dirección I de la onda incidente y la dirección R de la onda 
reflejada, forman el mismo ángulo con la recta normal a la 
superficie del obstáculo. 
Cuando las ondas cambian de medio de propagación, 
también cambian de velocidad de propagación, lo que  origina el cambio de dirección conocido como refracción. 
Los ángulos de la onda incidente I con la normal a la 
superficie de separación  y de la onda refractada R con 
esta misma normal cumplen la ley de Snell  V1∙sen(I)  =V2∙sen(R) donde V1 y V2 son las velocidades de 

propagación en cada medio.
















0